Solved Holder's inequality: Starting from the theorem | Chegg.com
The Holder Inequality (L^1 and L^infinity) - YouTube
PDF) Some integral inequalities of Hölder and Minkowski type
Dan Sitaru's Integral Inequality with Powers of a Function
Solved Minkowski Inequality 1 p infinity. FINITE SUMS: | Chegg.com
Minkowski inequality - Wikipedia
Solved Fix p,q > 1 such that 1/p + 1/q = 1. Then Holder's | Chegg.com
The Holder Inequality (L^p and L^q spaces) - YouTube
Solved 1. Holder's integral inequality if defined as: | Chegg.com
real analysis - Special case in proof of Holder's inequality - Mathematics Stack Exchange
calculus - Equality case in elementary form of Holder's Inequality - Mathematics Stack Exchange
![SOLVED: Prove the following integral version of Minkowski s inequality for 1 < p and a measurable function f (x,y): 1/p 1/p [S [fvox;y)ax]? dy]' <S [fte;y)1 dy]] dx (For 1 <p <](https://cdn.numerade.com/ask_images/3639f365d71745b1ac6f6a41e9d42cb4.jpg "SOLVED: Prove the following integral version of Minkowski s inequality for 1 < p and a measurable function f (x,y): 1/p 1/p [S [fvox;y)ax]? dy]' <S [fte;y)1 dy]] dx (For 1 <p <")
SOLVED: Prove the following integral version of Minkowski s inequality for 1 < p and a measurable function f (x,y): 1/p 1/p [S [fvox;y)ax]? dy]' <S [fte;y)1 dy]] dx (For 1 <p <
measure theory - Holder inequality is equality for $p =1$ and $q=\infty$ - Mathematics Stack Exchange
Ostrowski type fractional integral inequalities for s -Godunova-Levin functions via k -fractional integrals
PDF) Integral inequalities | Linh Bùi - Academia.edu
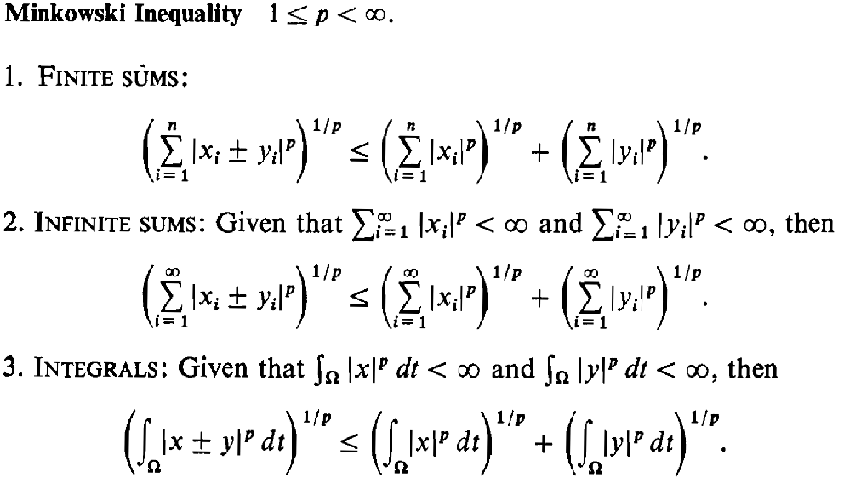
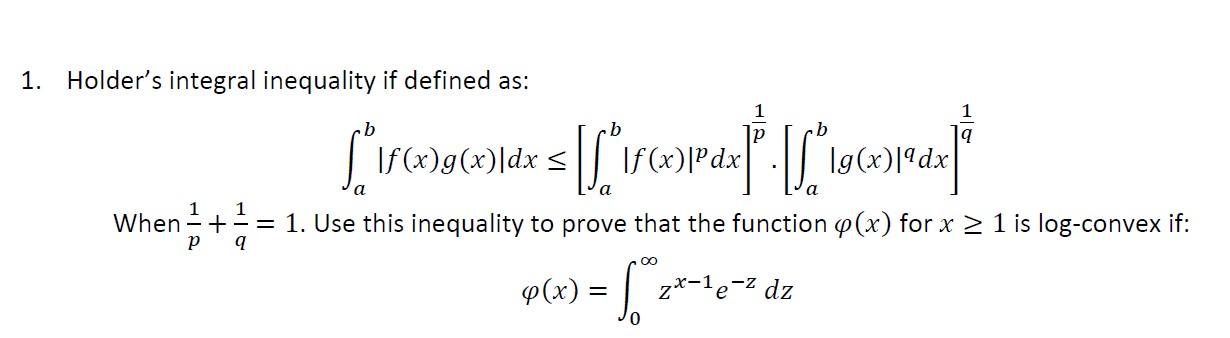
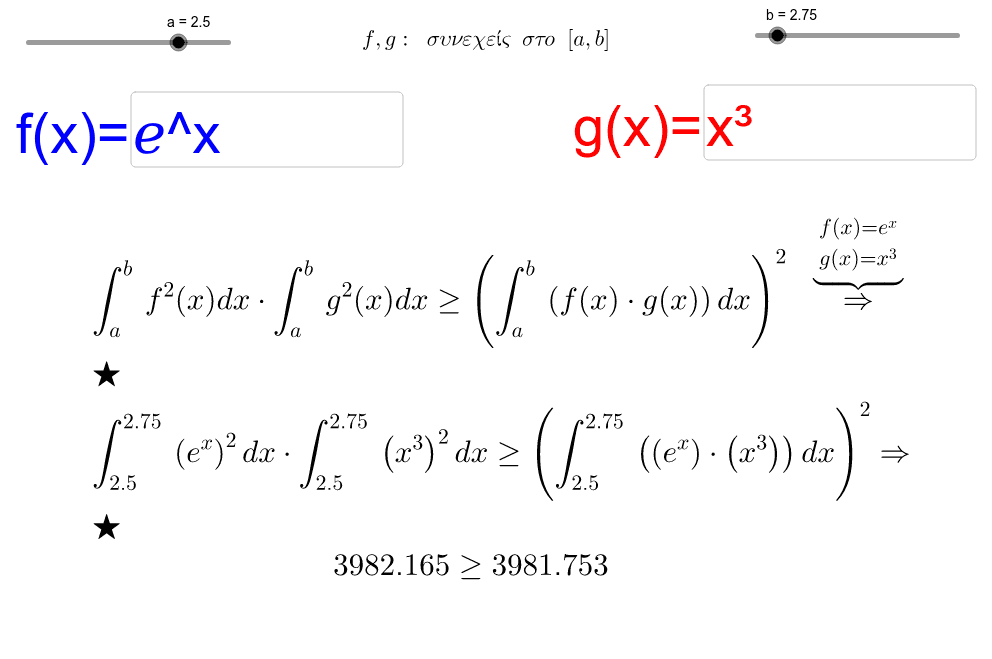
Cauchy-Schwarz Inequality for Integrals – GeoGebra
PDF) NEW REFINEMENTS FOR INTEGRAL AND SUM FORMS OF HÖLDER INEQUALITY
An Improvement of Minkowski's Inequality for Sums | Scientific.Net
Sam Walters ☕️ on Twitter: "The Hölder Inequality that is known for integrals also holds for traces of matrices. (Another reason why the trace behaves like integration, and it's one part of
![Solved (5) (i) (Cauchy-Schwarz inequality). Let f,g : a,b] → | Chegg.com](https://d2vlcm61l7u1fs.cloudfront.net/media%2F44e%2F44e44055-6a4d-4d95-b3b8-ee8d76283cb5%2FphpReQYBi.png "Solved (5) (i) (Cauchy-Schwarz inequality). Let f,g : a,b] → | Chegg.com")
Solved (5) (i) (Cauchy-Schwarz inequality). Let f,g : a,b] → | Chegg.com
Holder's Inequality (Functional Analysis) - YouTube
PDF) On Minkowski and Hardy integral inequalities | Lazhar BOUGOFFA - Academia.edu
real analysis - Proof of Hölder's inequality for improper integrals - Mathematics Stack Exchange
103.35 Hölder's inequality revisited | The Mathematical Gazette | Cambridge Core
PDF) The generalized Holder's inequalities and their applications in martingale spaces
